计数排序·CountingSort
计数排序是一个非基于比较的排序算法,该算法于 1954 年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时,它的复杂度为 Ο(n+k)(其中 k 是整数的范围),快于任何比较排序算法。
当然这是一种牺牲空间换取时间的做法,而且当 O(k)>O(n*log(n))的时候其效率反而不如基于比较的排序(基于比较的排序的时间复杂度在理论上的下限是 O(n*log(n)), 如归并排序,堆排序)
算法原理
取最大值和最小值,统计元素出现次数,计数累加,反向填充输出
- 找出待排序的数组中最大和最小的元素;
- 统计数组中每个值为 i 的元素出现的次数,存入数组 C 的第 i 项;
- 对所有的计数累加(从 C 中的第一个元素开始,每一项和前一项相加);
- 反向填充目标数组:将每个元素 i 放在新数组的第 C(i)项,每放一个元素就将 C(i)减去 1。
算法演示
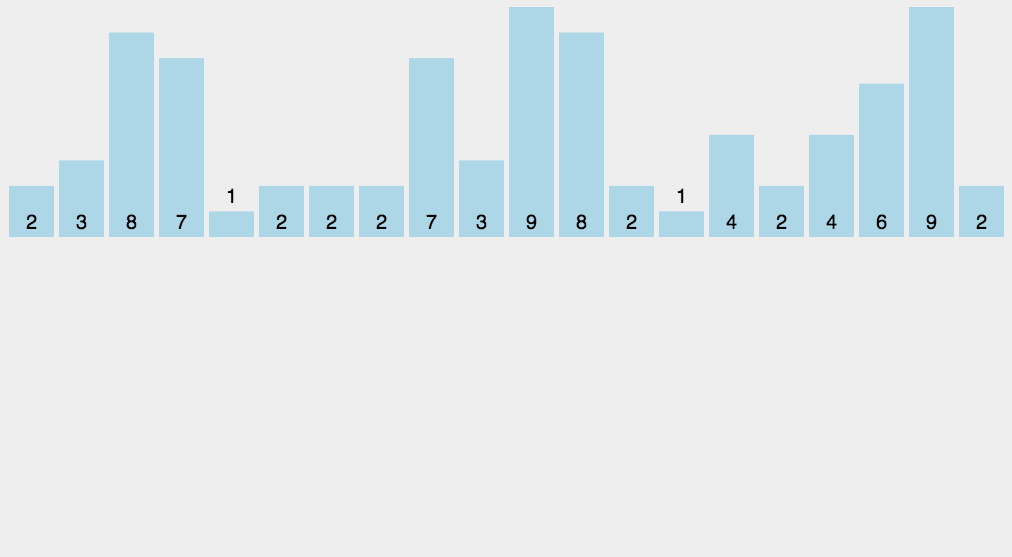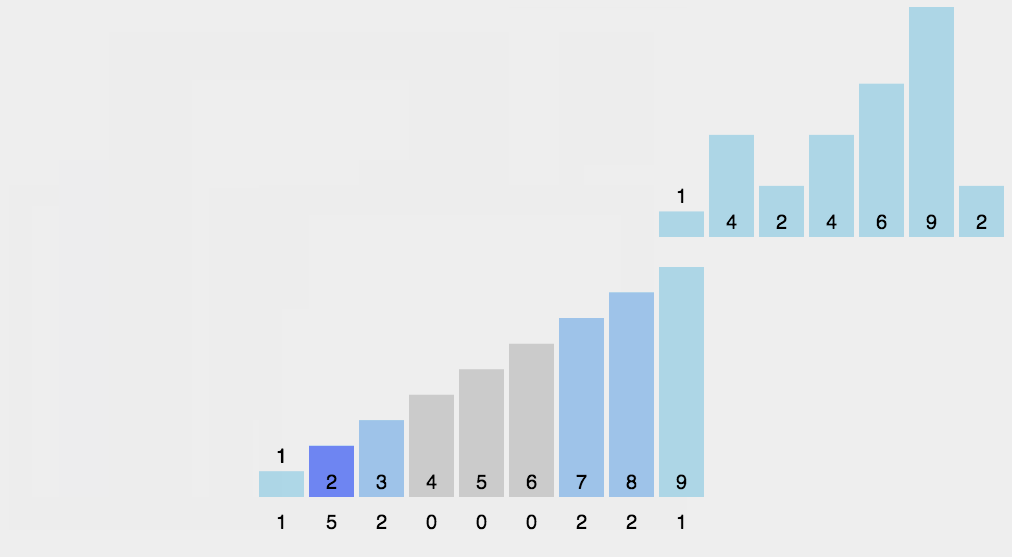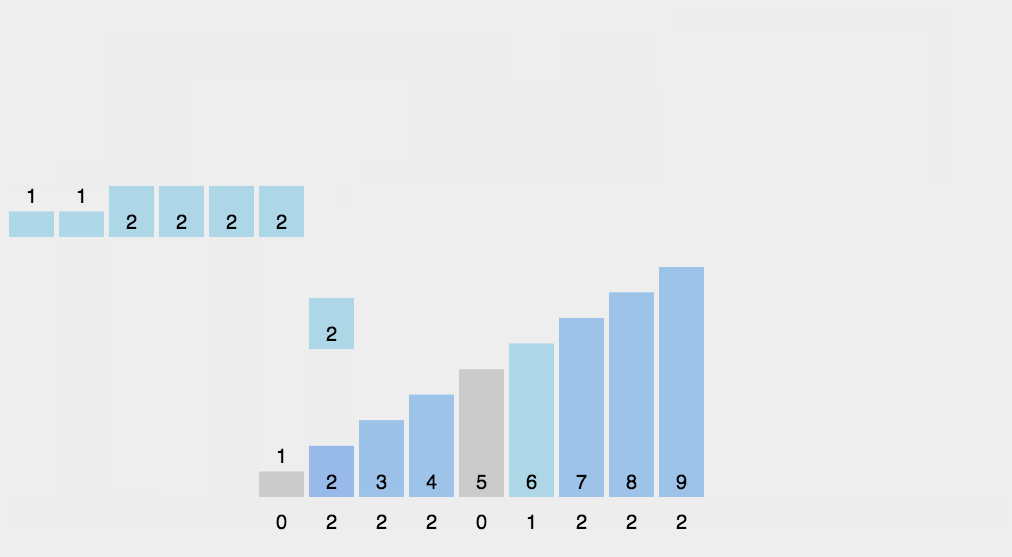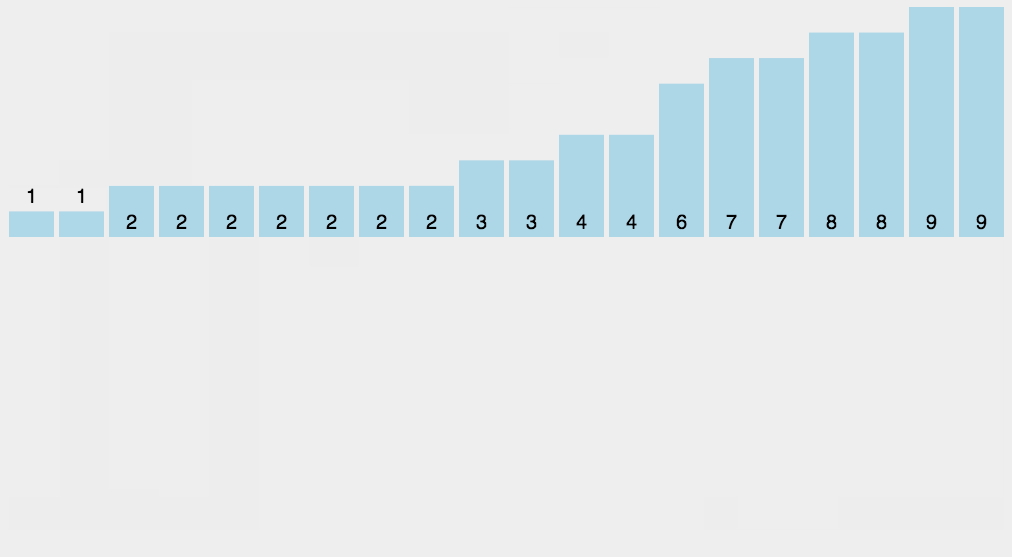
算法分析
时间复杂度
- 最好时间复杂度 O(n+k)
- 最坏时间复杂度 O(n+k)
- 平均时间复杂度 O(n+k)